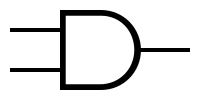
The basic logic gates are AND, OR, NOT and XOR. The AND gate is an electronic circuit that gives a high output (1) only if all its inputs are high. The diagram is the following:

For describing the functionality of the circuit we use truth tables, which can be extended or reduced. We can in fact provide the functionality of the circuit by giving a partial specification. If we provide the on-set truth table, we provide the values for which our circuit will respond with high output (1). Vice-versa when we provide the values for 0, we are describing the off-set.
In the case of the AND gate, the extended truth table is this one:

Inputs		Output
A	B	C
0	0	0
0	1	0
1	0	0
1	1	1

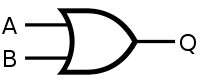
The OR gate is an electronic circuit that gives a high output (1) if one or more of its inputs are high. The diagram is the following:

And here is the extended truth table:

Inputs		Output
A	B	C
0	0	0
0	1	1
1	0	1
1	1	1

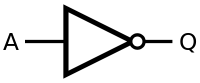
The NOT gate is an electronic circuit that produces an inverted version of the input at its output. The diagram is the following:

And here is the extended truth table:

Input	Output
A	C
0	1
1	0

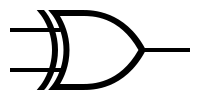
The XOR gate is a circuit which will give a high output if either, but not both, of its two inputs are high. The diagram is the following:

And here is the extended truth table:

Inputs		Output
A	B	C
0	0	0
0	1	1
1	0	1
1	1	0

But how can we represent those things inside SIS? Through BLIF files! BLIF stands for Berkeley Logic Interchange Format and it's a specification for describing sequential circuit logic. The format is easy to understand, so let's start. Here is the BLIF file of and AND gate.

# This is an AND gate
.model AND

.inputs A B
.outputs X

.names A B X
11 1

.end

Let's take a closer look at it. When a word start with a point ., it means it's a keyword. When it starts with a hash #, it's a comment. The first instruction, .model, declares the name of the model. While it's not mandatory, it's very recommended to declare it (otherwise you couldn't reuse it later, see the full adder tutorial). The .inputs and the .outputs instruction are self-explanatory. The .names instruction tells SIS we're going to write a partial truth table. Please note that SIS will complain if we deliver the extended truth table, so we choose if we want to provide the on-set or the off-set and we write down the partial truth table. In case of the AND port it's convenient to write the on-set (it's only one row!). As you can see we write the inputs close together and the output is separated with a blank space. SIS support only one output at a time, so if we need to deliver more outputs, we'll need to use more .names. We can also use temporary variables to store the output, the important thing is that if we declared X to be the output, at some point a .names structure will have to deliver it.

So we are now able to write down the other three port. The OR port (off-set table):

# This is an OR gate
.model OR

.inputs A B
.outputs X

.names A B X
00 0

.end

The NOT port (on-set table):

# This is a NOT gate
.model NOT

.inputs A
.outputs B

.names A B
0 1

.end

The XOR port (on-set table):

# This is a XOR gate
.model XOR

.inputs A B
.outputs X

.names A B X
01 1
10 1

.end

We can easily test the models with the sim command, which allows to simulate an input. For doing that, open up SIS in the same directory where the .blif file is stored, load that file with read_blif [FILE_NAME].blif command, and then you can run the simulation.

UC Berkeley, SIS 1.4 (compiled 2018-10-15 16:08:57)
sis> read_blif and.blif
sis> sim 0 1

Network simulation:
Outputs: 0
Next state:
sis> sim 1 1

Network simulation:
Outputs: 1
Next state:
sis> read_blif or.blif
sis> sim 1 0

Network simulation:
Outputs: 1
Next state:
sis> read_blif xor.blif
sis> sim 1 1

Network simulation:
Outputs: 0
Next state:
sis> sim 0 1

Network simulation:
Outputs: 1
Next state:
sis> read_blif not.blif
sis> sim 1

Network simulation:
Outputs: 0
Next state:
sis>